Table of Contents
モチベーション
散布図から関数を予測したい
scikit-learnのLinearRegressionで単回帰する
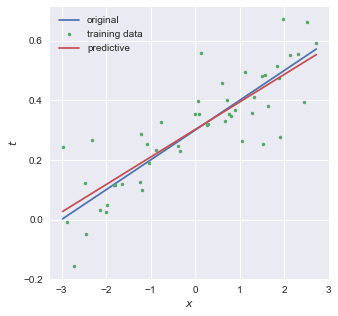
-3 < x < 3 の範囲でxをランダムに50点生成し, $y=0.1x+0.3$ に入力した後,yにσ=0.1のガウシアンノイズを加えたtを教師データとした.青線(original)が直線y,散布図(training data)がtである.
scikit-learnのLinearRegressionを用いて $y=0.1x+0.3$ を予測したものが赤線 (predictive) である.
coefficientは0.09くらい,interceptは0.30くらいとなり, $y=0.09x+0.30$ と予測できた.
import numpy as np
from matplotlib import pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from matplotlib.colors import ListedColormap
colors = ['#e74c3c', '#3498db', '#1abc9c', '#9b59b6', '#f1c40f'] # red, blue, green, purple, yellow
cmap = ListedColormap(colors)
plt.style.use('seaborn')
def f(x):
return 0.1*x + 0.3
N = 50
X = np.zeros((N,1))
np.random.seed(seed=10)
X[:,0] = np.random.uniform(-3, 3, N)
noise = 0.1*np.random.randn(N) # σ=0.1
t = f(X[:,0])+ noise
X_train, X_test, t_train, t_test = train_test_split(X, t, random_state=0)
lr = LinearRegression().fit(X_train, t_train)
print("train R^2:", lr.score(X_train, t_train))
print("test R^2:", lr.score(X_test, t_test))
print(f"coefficient:{lr.coef_} intercept:{lr.intercept_}")
fig = plt.figure(figsize=(5,5))
Xcont = np.linspace(np.min(X), np.max(X), 200)
plt.plot(Xcont, f(Xcont), label='original')
plt.plot(X, t,'.', label='training data')
plt.plot(Xcont, lr.coef_[0]*Xcont+lr.intercept_, label='predictive')
plt.xlabel(r'$x$')
plt.ylabel(r'$t$')
plt.legend()
plt.show()二乗和誤差を小さくするような係数を探す
$x_n$ を入力すると予測値 $y(x_n, \boldsymbol{w})$ が得られるような関数をつくりたい.そのためには,係数 $w_0, w_1$ を求める必要がある.
以下の二乗和誤差が小さくなるような係数 $w$ を探す.
$C^2$ 級(2階連続微分可能)な関数 $z=f(x,y)$ が $(a,b)$ で極値を持つとき, $f_x(a,b)=f_y(a,b)=0$ が成り立つが,極小か極大か鞍点であるかは断言できないことに注意する.断言したいなら,以下のヘッセ行列 $H$ について
- $f_{xx}(a,b) > 0$かつ$|H| > 0$(正定値)であるなら,$z$ は $(a,b)$ で極小値をとる.
- $f_{xx}(a,b) < 0$かつ$|H| < 0$(負定値)であるなら,$z$ は $(a,b)$ で極大値をとる.
- $|H| < 0$であるなら,$z$は$(a,b)$で極小をとらない.
を評価する必要がある.
結局のところ,$E(\boldsymbol{w})$ は極小値を持つので, $\frac{ \partial E(\boldsymbol{w}) }{ \partial w_0 }=0$ と $\frac{ \partial E(\boldsymbol{w}) }{ \partial w_1 }=0$ を求めると以下のように整理できる.$(x_n,t_n)$ は教師データセットであり,Nは教師データ数である.
scikit-learnのLinearRegressionで重回帰する
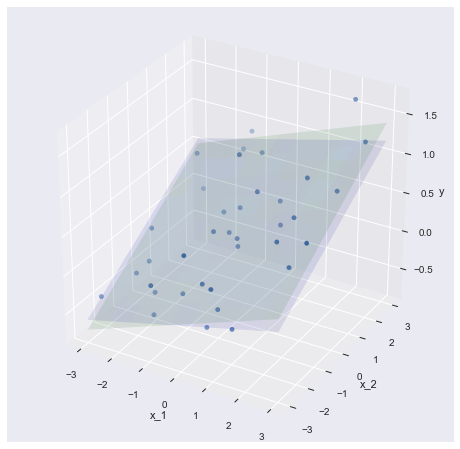
$-3 < x_1 < 3, -3 < x_2 < 3$ の範囲で $x_1,x_2$ をそれぞれランダムに50点生成し, $y=0.1x_1+0.2x_2+0.3$ に入力した後,yにσ=0.3のガウシアンノイズを加えたtを教師データとした.青面がy平面,散布図がtである.
scikit-learnのLinearRegressionを用いて $y=0.1x_1+0.2x_2+0.3$ を予測したものが緑面である.
coefficientは0.15, 0.21くらい,interceptは0.35くらいとなり, $y=0.15x+0.21x+0.35$ と予測できた.
import numpy as np
from matplotlib import pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.colors import ListedColormap
colors = ['#e74c3c', '#3498db', '#1abc9c', '#9b59b6', '#f1c40f'] # red, blue, green, purple, yellow
cmap = ListedColormap(colors)
plt.style.use('seaborn')
def f(x1,x2):
return 0.1*x1 + 0.2*x2 + 0.3
N = 50
X = np.zeros((N,2))
np.random.seed(seed=2)
X[:,0] = np.random.uniform(-3, 3, N)
X[:,1] = np.random.uniform(-3, 3, N)
noise = 0.3*np.random.randn(N) # σ=0.3
t = f(X[:,0],X[:,1])+ noise
X_train, X_test, t_train, t_test = train_test_split(X, t, random_state=0)
fig = plt.figure(figsize=(8,8))
ax = fig.add_subplot(1,1,1, projection='3d')
ax.scatter(X_train[:,0], X_train[:,1], t_train)
lr = LinearRegression().fit(X_train, t_train)
coef = lr.coef_
line = lambda x1, x2: f(x1,x2)
grid_x1, grid_x2 = np.mgrid[-3:3:10j, -3:3:10j]
ax.plot_surface(grid_x1, grid_x2, line(grid_x1, grid_x2), alpha=0.1, color='b')
coef = lr.coef_
line = lambda x1, x2: coef[0] * x1 + coef[1] * x2 + lr.intercept_
grid_x1, grid_x2 = np.mgrid[-3:3:10j, -3:3:10j]
ax.plot_surface(grid_x1, grid_x2, line(grid_x1, grid_x2), alpha=0.1, color='g')
ax.set_xlabel("x_1")
ax.set_ylabel("x_2")
ax.set_zlabel("y")
plt.show()
print("train R^2:", lr.score(X_train,t_train))
print("test R^2:", lr.score(X_test,t_test))
print(f"coefficient:{lr.coef_} intercept:{lr.intercept_}")単回帰と同様,二乗和誤差を小さくするような係数を探す
単回帰では1種類の $x$ からyを予想したのに対し,重回帰では複数種類の $x$ から $y$ を予想する.
$\boldsymbol{x_n}^{\mathrm{T}} = (1, x_{n1} , x_{n2}, …, x_{nD})$ を入力すると予測値 $y(\boldsymbol{x_n}, \boldsymbol{w})$ が得られるような関数をつくりたい.そのためには,係数 $\boldsymbol{w}^{\mathrm{T}} = (w_0, w_1, …, w_D)$ を求める必要がある.
複数の教師データセット $(\boldsymbol{x_n}, t_n)$ を入力し,以下の二乗和誤差が小さくなるような係数 $\boldsymbol{w}$ を探す.Nは教師データ数である.
今回はベクトルを含んだ計算が必要なので,少々トリッキーになる.
一般に,ベクトル $\boldsymbol{b}^{\mathrm{T}} = (a_1, a_2, \ldots, a_N)$ の各スカラーの二乗和 $\sum_{i=1}^{N} a_i^2$ は,
である.また, $\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x_n} = \boldsymbol{x_n}^{\mathrm{T}} \boldsymbol{w}$ の性質と計画行列 $\boldsymbol{X}$ を用いると以下のように変形できる.
これにより,
と変形できる.
$(\boldsymbol{AB})^{\mathrm{T}} = \boldsymbol{B}^{\mathrm{T}} \boldsymbol{A}^{\mathrm{T}}$ の性質を用いると,
と展開できる.これを $\boldsymbol{w}$ に関して偏微分することで最小値を求める.まずは第二項目について考える.
$\boldsymbol{a}^{\mathrm{T}} = (a_0, a_1, \ldots, a_D)$と$\boldsymbol{w}^{\mathrm{T}} = (w_0, w_1, \ldots, w_D)$ とおくと,
という性質があるので,
と求まる.次に,第一項目に関して考える.
一般的な $\boldsymbol{w}$ の二次形式 $\boldsymbol{w}^{\mathrm{T}} A \boldsymbol{w}$ について, $N \times N$の行列$A_{行,列}$ を用いて級数で表す.
これを $w_k$ で微分してみる.
「$w_k$ かけるなんちゃら」が2ペアできることがミソ.
(k,:)はnumpyのスライスと同義であり,k行の全列を抜き出した行ベクトルを表す. $\boldsymbol{w}$ で偏微分するように拡張すると,
これでやっと,二乗和誤差の $\boldsymbol{w}$ に関する偏微分が完了する.
$X^{\mathrm{T}} X$ が逆行列をもつとして, $\frac{ \partial }{ \partial \boldsymbol{w} } E(\boldsymbol{w}) = 0$ を解くと,係数ベクトル $\boldsymbol{w}$ が求まる.
線形モデルで非線形を表現する
ここまでは,入力 $x_n$ を定数倍することで予測関数をつくっていたため,以下のような二次関数を予測するにはなにか別の手段を考える必要がある.
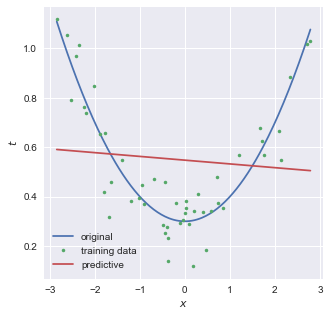
結論から言うと,以下のようなモデルについて考えれば良い.
より一般化すると, $\boldsymbol{x_n}^{\mathrm{T}} = (1, x_{n1} , x_{n2}, …, x_{nD})$ を入力すると予測値 $y(\phi(\boldsymbol{x_n}), \boldsymbol{w})$ が得られるような関数を $\boldsymbol{w}^{\mathrm{T}} = (w_0, w_1, …, w_D)$ を用いてつくればよい.
$\boldsymbol{x_n} =x_n$ , $\boldsymbol{\phi(x)} = (1, x, x^2)$ とすると,前述した二次関数を表現することができる.
教師データを複数入力する際は,以下のような計画行列 $\Phi$ を用いるとよい.
$\boldsymbol{w}$ の求め方は,これまでと同様である.
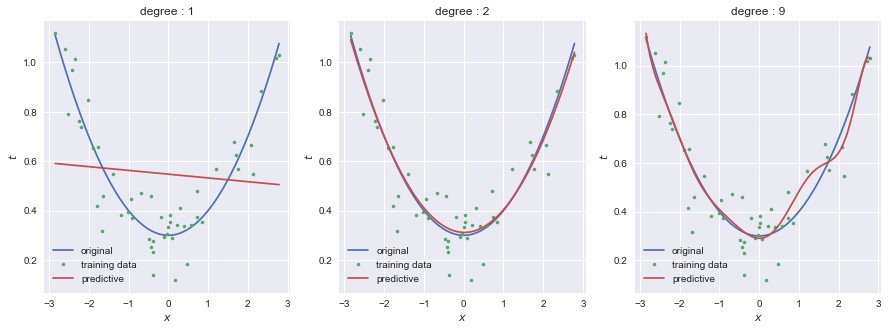
scikit-learnのPolynomialFeaturesを用いることで,モデルの次数を自由に変えることができる.以下は1次,2次,9次の3つのモデルの結果である.
import numpy as np
from matplotlib import pyplot as plt
from sklearn.linear_model import LinearRegression
from matplotlib.colors import ListedColormap
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.model_selection import train_test_split
colors = ['#e74c3c', '#3498db', '#1abc9c', '#9b59b6', '#f1c40f'] # red, blue, green, purple, yellow
cmap = ListedColormap(colors)
plt.style.use('seaborn')
def f(x):
return 0.1*x**2 + 0.3
N = 50
X = np.zeros((N,1))
np.random.seed(seed=2)
X[:,0] = np.random.uniform(-3, 3, N)
noise = 0.1*np.random.randn(N) # σ=0.1
t = f(X[:,0])+ noise
X_train, X_test, t_train, t_test = train_test_split(X, t, random_state=0)
fig, ax = plt.subplots(1, 3, figsize = (15, 5))
for degree, ax in zip([1,2,9], ax):
pipeline = Pipeline([
('polynominal_features', PolynomialFeatures(degree=degree)),
('linear_regression', LinearRegression())
])
lr = pipeline.fit(X_train, t_train)
print("train R^2:", lr.score(X_train, t_train))
print("test R^2:", lr.score(X_test, t_test))
print(pipeline.steps[1][1].coef_)
Xcont = np.linspace(np.min(X), np.max(X), 200).reshape((200, 1))
ax.plot(Xcont, f(Xcont), label='original')
ax.plot(X, t,'.', label='training data')
ax.plot(Xcont, lr.predict(Xcont), label='predictive')
ax.set_title('degree : {}'.format(degree))
ax.legend()
ax.set_xlabel(r'$x$')
ax.set_ylabel(r'$t$')$\boldsymbol{\phi(x)} = (1, x, sin(x))$ のようにすることで,三角関数を含んだモデルを構築することができる.が,自身での実装が必要になる.
正則化項を導入することで過学習を抑える
0 < x < 1 の範囲でxをランダムに10点生成し, $y=sin(2\pi x)$ に入力した後,yにσ=0.2のガウシアンノイズを加えたtを教師データとした.青線が関数y,散布図がtである.
scikit-learnのLinearRegressionとPolynomialFeaturesを用いて,1次,3次,9次のモデルによって $y=sin(2\pi x)$ を予測したものが赤線である.
9次において,教師データに過剰に適合しようとしていることがわかる.これが過学習(過適合,over-fitting)である.
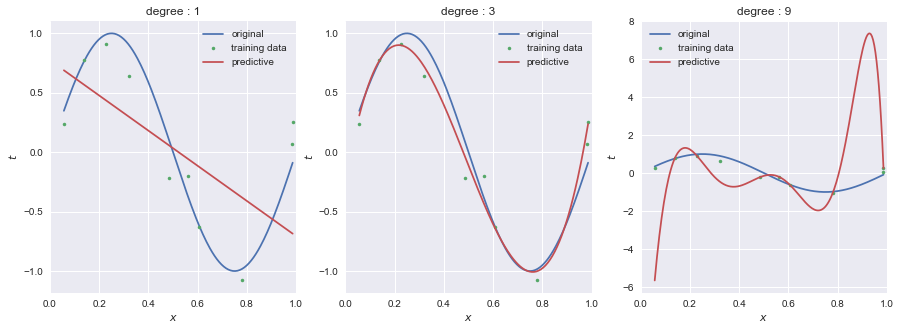
次数を小さくする(=モデルをシンプルにする)ことで過学習を避けることが期待できるが,うまい次数を探す必要がある.
教師データを増やすことで過学習を避けることができる.教師データ数を10組から100組に増やした例が以下であり,9次のモデルでも予測できている.
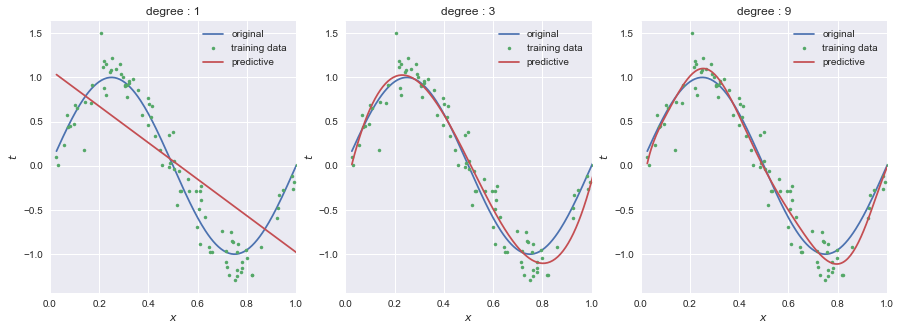
教師データが大量に手に入る場合はいいかもしれないが,限られた量しか手に入らない場合は断念しなければならないといった問題がある.
ここで,各次数のモデルにおける係数$w$を見てみる.
| $w_0$ | $w_1$ | $w_2$ | $w_3$ | $w_4$ | $w_5$ | $w_6$ | $w_7$ | $w_8$ | $w_9$ |
|---|---|---|---|---|---|---|---|---|---|
| 0.0 | -2.1 | ||||||||
| 0.0 | 12.6 | -35.3 | 22.7 | ||||||
| 0.0 | 22.2 | -263.1 | 2140.3 | -9774.9 | 25228.6 | -38193.9 | 33691.2 | -16021.9 | 3171.9 |
過学習である/ないに関わらず,モデルの次数が大きくなるほど係数wが大きくなっている.つまり,小さいノイズが誇張されてしまうので,過学習が発生すると考えることができる.
より論理的には, $\boldsymbol{w}$ を求める際に, $\Phi^{\mathrm{T}} \Phi$ の逆行列ギリギリ求められるか求められない場合に起こる.例えば, $\boldsymbol{x_n}$ の各スカラー間に相関がある場合や $\boldsymbol{x_n}$ の要素数が教師データ数より多いときに計画行列のランクが落ちてしまうので逆行列を持てなくなってしまう.
そこで,単位行列$I$を導入することで逆行列を確実に持つようにする.これを正則化という.
これは,以下の二乗和誤差を最小にする値である. $ \| \boldsymbol{w} \| = \boldsymbol{w}^{\mathrm{T}}\boldsymbol{w} $ である.これをRidge回帰という.
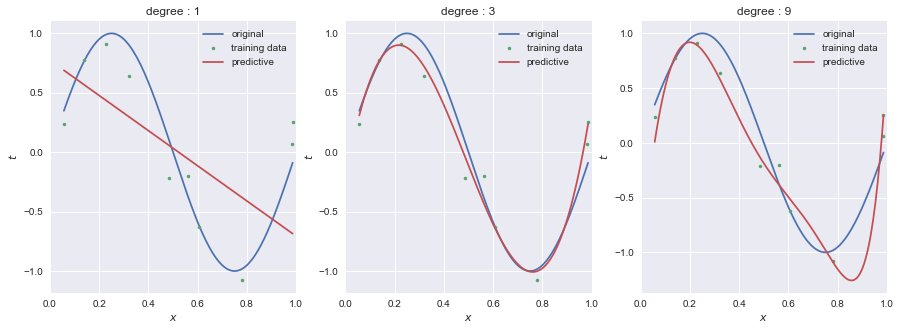
scikit-learnのRidgeを用いてRidge回帰を行った結果が以下である.過学習が抑えられている.
Ridgeには, $\lambda$ に相当するalphaというパラメータがあり,今回はalpha=0.0000001と指定した.この$\lambda$の値をどのように探すかは,後ほど述べることにする.
9次のモデルにおいて, $\boldsymbol{w}$ を見ると,(0.0, 23.7, -87.5, 91.0, 24.7, -51.1, -40.1, 10.9, 34.7, -4.4)というように,比較的小さな値に抑えられている.
import numpy as np
from matplotlib import pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import Ridge
colors = ['#e74c3c', '#3498db', '#1abc9c', '#9b59b6', '#f1c40f'] # red, blue, green, purple, yellow
cmap = ListedColormap(colors)
plt.style.use('seaborn')
def f(x):
return np.sin(2*np.pi*x)
N = 10
X = np.zeros((N,1))
np.random.seed(seed=3)
X[:,0] = np.random.uniform(0, 1.1, N)
noise = 0.2*np.random.randn(N) # σ=0.2
t = f(X[:,0])+ noise
X_train, X_test, t_train, t_test = train_test_split(X, t, random_state=0)
fig, ax = plt.subplots(1, 3, figsize = (15, 5))
for degree, ax in zip([1,3,9], ax):
pipeline = Pipeline([
('polynominal_features', PolynomialFeatures(degree=degree)),
('ridge', Ridge(alpha=0.0000001))
])
lr = pipeline.fit(X_train, t_train)
print("train R^2:", lr.score(X_train, t_train))
print("test R^2:", lr.score(X_test, t_test))
print(pipeline.steps[1][1].coef_)
Xcont = np.linspace(np.min(X), np.max(X), 200).reshape((200, 1))
ax.plot(Xcont, f(Xcont), label='original')
ax.plot(X, t,'.', label='training data')
ax.plot(Xcont, lr.predict(Xcont), label='predictive')
ax.set_xlim(0.0, 1.0)
ax.set_title('degree : {}'.format(degree))
ax.legend()
ax.set_xlabel(r'$x$')
ax.set_ylabel(r'$t$')