Table of Contents

モチベーション

scikit-learnのDecisionTreeClassifierで分類する

2つの特徴量 $X_0,X_1$ からなる，以下のようなデータセットを分類したい．

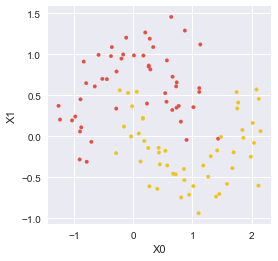
dataset_moon

from sklearn.datasets import make_moons
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap

# style
colors = ['#e74c3c', '#3498db', '#1abc9c', '#9b59b6', '#f1c40f'] # red, blue, green, purple, yellow
cmap = ListedColormap(colors)
plt.style.use('seaborn')

X, y = make_moons(n_samples=100, noise=0.25, random_state=0)

plt.figure(figsize=(4,4))
plt.scatter(X[:,0], X[:,1], c=y, cmap=cmap, marker='.')
plt.ylabel('X0')
plt.xlabel('X1')


plt.show()

scikit-learnのDecisionTreeClassifierで分類した結果が以下である．

from sklearn.datasets import make_moons
from matplotlib.colors import ListedColormap
from sklearn.tree import DecisionTreeClassifier, export_graphviz
import pydotplus
import matplotlib.pyplot as plt
import numpy as np

# style
colors = ['#e74c3c', '#3498db', '#1abc9c', '#9b59b6', '#f1c40f'] # red, blue, green, purple, yellow
cmap = ListedColormap(colors)
plt.style.use('seaborn')

def paint_classified_area(ax, clf, X, t, nx=100, ny=100, margin=0.1):
    x_min, x_max = (1 + margin) * X[:,0].min() - margin * X[:,0].max(), (1 + margin) * X[:,0].max() - margin * X[:,0].min()
    y_min, y_max = (1 + margin) * X[:,1].min() - margin * X[:,1].max(), (1 + margin) * X[:,1].max() - margin * X[:,1].min()
    xx, yy = np.meshgrid(np.linspace(x_min, x_max, nx), np.linspace(y_min, y_max, ny))
    Z = (clf.predict(np.c_[xx.ravel(), yy.ravel()])).reshape(xx.shape)
    ax.contourf(xx, yy, Z, alpha=0.1, colors=colors)

def export_tree_graph(graph_name, features, classes):
    dot_name="./dtc.dot"
    export_graphviz(dtc, 
                    out_file=dot_name, 
                    impurity = False, 
                    filled = False,
                    class_names=classes,
                    feature_names=features)
    graph = pydotplus.graph_from_dot_file(dot_name)
    graph.write_png(graph_name)

fig, ax = plt.subplots(1, 3, figsize = (15, 5))

X, y = make_moons(n_samples=100, noise=0.25, random_state=0)
for max_depth, ax in zip([1,3,9], ax):
    dtc = DecisionTreeClassifier(criterion="entropy",max_depth=max_depth, random_state=0)
    dtc.fit(X, y)
    print("accuracy:{:.3f}".format(dtc.score(X, y)))

    paint_classified_area(ax, dtc, X, y)
    
    ax.scatter(X[:,0], X[:,1], c=y, cmap=cmap, marker='.')
    ax.set_title('max_depth : {}'.format(max_depth))
    ax.set_xlabel("X [0]")
    ax.set_ylabel("X [1]")
    
    export_tree_graph(
        graph_name = "dtc{}.png".format(max_depth),
        features = ["X[0]","X[1]"],
        classes = ["upper","lower"])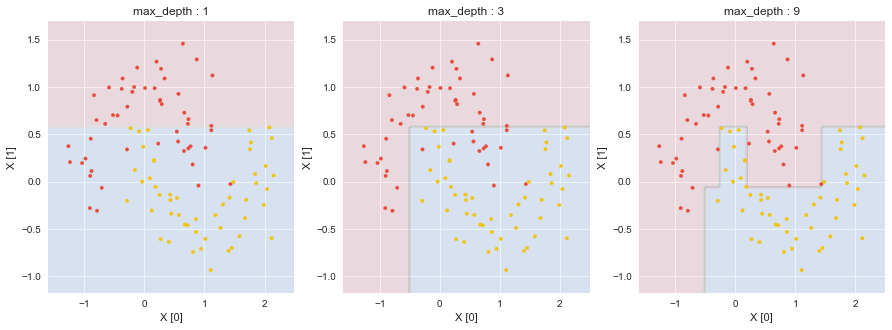

decision_tree_139

dtc139

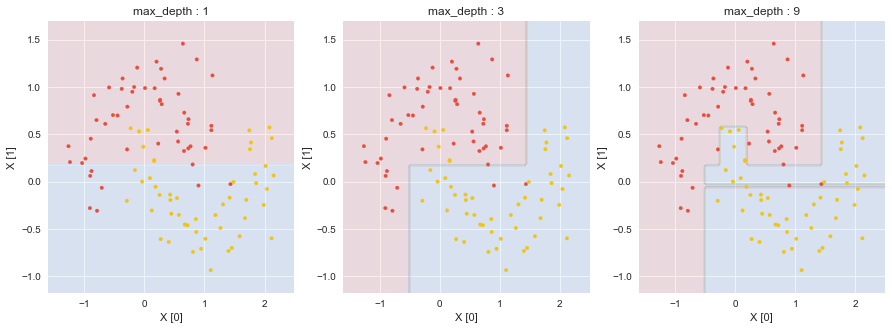
DecisionTreeClassifierのcriterionとしてentropyを指定した．最大深さ9の決定木について，深さ6で葉が純粋になっている．

DecisionTreeClassifierの.score(X, y)にて，データへのフィッティング具合を知ることができる．今回は0.780, 0.880, 1.000であり，最大深さ９の場合が（訓練データセットに）一番フィットしている事になった．ただし，.score(X, y)が大きいからと言って，未知データの予測精度が高いわけではないことに注意する．訓練データセットに過剰適合していることが常である．

DecisionTreeClassifierの.feature_importances_にて，分割に貢献している特徴量を知ることができる．最大の深さが1の場合の.feature_importances_は[0. 1.]となり，特徴量X1で分割されたことが反映されている．また，最大深さが9の場合の.feature_importances_は[0.49836396 0.50163604]となり，特徴量X0とX1でまんべんなく分割されていることが反映されている．

「エントロピー」で「情報のあいまいさ」を表現する

「情報のあいまいさ」を定量的に表すことについて考えてみる．

コインを投げて表が出る確率は1/2であり，６面のサイコロを投げて１の目が出る確率は1/6である．感覚としては，コインの表裏を予想するよりもサイコロの目を予想する方が「あいまいさ」が増す． また，サイコロを２回投げる場合を予想するとなると，１回分を予想するよりもあいまいになった気がする．

サイコロを投げる事象は独立であるので，サイコロを２回投げたときに出る目は，1/6と1/6の積をとり，1/36の確率で予想できることになる．確率は低くなったが，あいまいさが増したと感じる．

ここまでの話を一般化すると，xが起きる確率をp(x)とおくと，２つの事象x,yが独立なら，p(x,y)=p(x)p(y)が成り立ち，また，x事象に関するあいまいさをh(x)とすると，２つの独立な事象x,yに関して，h(x,y)=h(x)+h(y)が成り立つような「何か」が欲しいということになる．ということで先人は以下の式を情報のあいまいさとした．

$$ h(x)=-\log_2 {p(x)} $$

これなら，確率が低ければ低いほどあいまいになることを表現できるし，確率の積によってあいまいさの和を表現することもできる．対数の底は何でもよく，２にすることが多いらしい．h(x)の単位はbit．

ここで，８つの文字{a,b,c,d,e,f,g,h}を袋に詰め，袋から１文字を取り出すクソゲーをする．８文字それぞれが1/8の確率で取り出せることが保証されている場合，１文字あたりの情報のあいまいさは3bitなので，８文字ぶんのあいまいさの期待値（平均）をとると，このクソゲーの「あいまいさの平均」は3bitとなる． 一方，{a,b,c,d,e,f,g,h}のそれぞれの確率が 1⁄2, 1⁄4, 1⁄8, 1⁄16, 1⁄64, 1⁄64, 1⁄64, 1⁄64 であるとすると，{a,b,c,d,e,f,g,h}のそれぞれの複雑さは1bit, 2bit, 3bit, 4bit, 6bit, 6bit, 6bit, 6bit となる．このあいまいさの期待値（平均）を計算すると2bitになるので，この場合のクソゲーの「あいまいさの平均」は2bitとなる．つまり，{a}が出やすいという情報を知ることで，あいまいさが減ったということを表している．

このような「あいまいさの平均」を情報エントロピーといい，各事象の確率次第で「あいまいさの平均」は変化することがわかる．

事象 $X_1,X_2,…,X_n$ のそれぞれの確率を $p_1,p_2,…,p_n$ とすると，全事象 $X$ のエントロピー $H[X]$ は以下で表せる．

$$ H[X]=-\sum_{n} p_i \log_2 {p_i} $$

事象 $X=X_1,X_2$ のそれぞれの確率を $p,p-1$ とした場合（＝ベルヌーイ分布に従う場合）のエントロピー $H[X]$ は次の図のように表せる．事象ごとの確率にばらつきがない場合にエントロピーが最も高くなり，ある事象だけ確率が極端に大きい/小さいときに，エントロピーが低くなることがわかる．表（または裏）のみが極端に出やすいコインはエントロピーが低く，表裏が等確率で出るコインはエントロピーが高い．

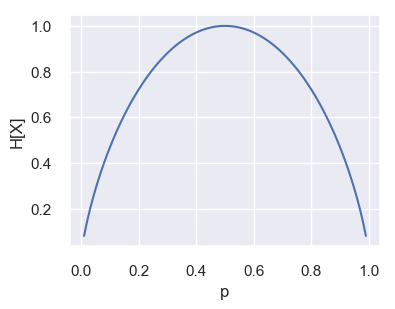
entropy

エントロピーの大小を基準にして決定木を構築する

エントロピーを求めるには，予め，各事象（各クラス）の確率（割合）を求めておく必要がある．

ノードmに属するクラスkの割合 $p(m,k)$ を求めるための式は以下である． $(x_i,y_i)$ は（特徴量，クラス），Rmはノード（葉）m内のデータ集合，Nmはノードmに属するすべてのデータ数を表す．

$$ p(m,k) = \frac{1}{N_m} \sum_{x_i \in R_m} I(y_i = k) $$

ノードmに関する情報エントロピーは以下の式で求められる．交差エントロピー誤差関数とも呼ぶ．

$$ H[X_m]=-　\sum_{k} p(m,k) \log_2 {p(m,k)} $$

分割前のデータセットをノード0とすると，ノード0のエントロピー $H[X_0]$ は1.0である．これは，クラスが未知の特徴量(X0,X1)が与えられたとき，この特徴量がクラス0なのかクラス1なのか見分けられない（あいまいさが大きい）ことを意味する．

早速，冒頭で紹介した月形のデータセットを分割していく．まず，特徴量X1に着目し，X1を降順にソートした上で，クラスを見てみる．

import pandas as pd

df = pd.DataFrame({"X0":X[:,0],"X1":X[:,1],"_class":y})
df.sort_values(by="X1", ascending=False).head(5)

X1が大きい部分はクラス0のみだが，X1が小さくなる方をみていくと，クラス1のデータが出てくる．

X0 X1 _class
-0.796819 0.649555 0
0.724286 0.610817 0
-0.652006 0.610241 0
1.114994 0.589595 0
2.081867 0.572525 1

とりあえず，分割軸をX1=0.589595とX1=0.572525の中間とする．

df.sort_values(by="X1", ascending=False).query('X1 > 0.581060').count()

X0       28
X1       28
_class    28

これで，28点のクラス0のみを含んだノード1と，22点のクラス0，50点のクラス1を含んだノード2に分割したことになる．

ノード1のエントロピー $H[X_1]$ は，ノード1内にクラス0しか含まれていないことから，0.0である．

ノード2のエントロピー $H[X_2]$ は $- \frac{22}{72} \log \frac{22}{72} - \frac{50}{72} \log \frac{50}{72} = 0.615498$ になる．

で，ノード0から各ノードにどれだけデータが分岐したのかを重み付けすることで，ノード1と2全体でのエントロピーを算出する．

$$ \frac{28}{100} H[X_1] + \frac{72}{100} H[X_2] = 0.443159 $$

この値はノード0の $H[X_0] = 1.0$ よりも小さいので，今回の分割によってあいまいさを小さくすることができたと言える．つまり，クラスが未知なデータ(X0,X1)が与えられたとき，X1が0.581060より大きな特徴量「クラス0だ」と予想でき，X1が0.581060より小さな特徴量は「クラス１である可能性が高い」と分類することができる．

元ノードと分岐後のノードのエントロピーの差分を「情報ゲイン」と言うらしい．情報ゲインが最大になるような分割軸を探していく．

試しに，更にX1が小さくなる方を見ていく．例えば，X1=0.18065とX1=0.164730の中間である0.172690らへんを分割軸にしてみる．

X0 X1 _class
0.162802 0.217376 1
-1.238857 0.205974 0
-1.036595 0.195670 0
0.803637 0.180650 0
2.017774 0.164730 1

X1 > 0.172690 なクラス0は43点，クラス1は11点あるらしい．

df.sort_values(by="X1", ascending=False).query('X1 > 0.172690')['_class'].value_counts()

0    43
1    11
Name: _class, dtype: int64

X1 = 0.172690 で分割された事によってできた２つの領域（ノード）について，それぞれエントロピーを求める．

$$ H[X_1] = - \frac{43}{54} \log \frac{43}{54} - \frac{11}{54} \log \frac{11}{54}　= 0.505494 $$
$$ H[X_2] = - \frac{7}{46} \log \frac{7}{46} - \frac{39}{46} \log \frac{39}{46}　= 0.426461 $$

元のノードから分岐したデータの割合で重み付けをする．

$$ \frac{54}{100} H[X_1] + \frac{46}{100} H[X_2] = 0.469137 $$

今回の情報ゲインは先に求めた情報ゲインよりも小さくなってしまったので，先程の分割の方が優秀であると言える．

X0についても同様に検証（分割テストと言う）していき，エントロピーが小さくなるような分割軸を探していく．

ここまでで，深さ（葉）が１の決定木ができたことになる．

ジニ不純度で決定木を構築する

DecisionTreeClassifierのcriterionには，”gini”が指定できる．

ノードmのジニ不純度 $H[X_m]$ は以下の式で与えられる．

$$ H[X_m] = \sum_{k} p_{mk} (1-p_{mk}) $$

$p_{mk}$ は先に述べたように，ノードmに属するクラスkの割合を表す． $(x_i,y_i)$ は（特徴量，クラス）， $R_m$ はノードm内のデータ集合， $N_m$ はノードmに属するすべてのデータ数を表す．

$$ p_{mk} = \frac{1}{N_m} \sum_{x_i \in R_m} I(y_i = k) $$

事象 $X=X_1,X_2$ のそれぞれの確率を $p,p-1$ とした場合（＝事象Xがベルヌーイ分布に従う場合）のジニ不純度とエントロピーをプロットしてみた．（ジニ不純度の最大値とエントロピーの最大値が一致するようにジニ不純度を２倍した）

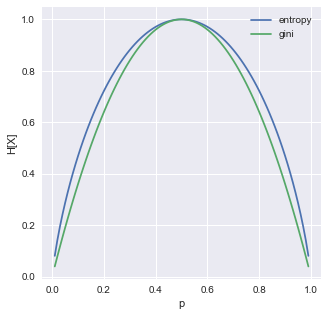
entropy_gini

ジニ不純度とエントロピーを比較すると，エントロピーのグラフはp=0.0と1.0付近が急峻であるため，ノードが純粋であることを好む．一方，ジニ不純度のグラフはp=0.0と1.0付近が緩やかであるが，0.5付近は急峻であるため，ノードが純粋であることは強要しないが，p=0.5付近は白黒つけるぞという気持ちがある．

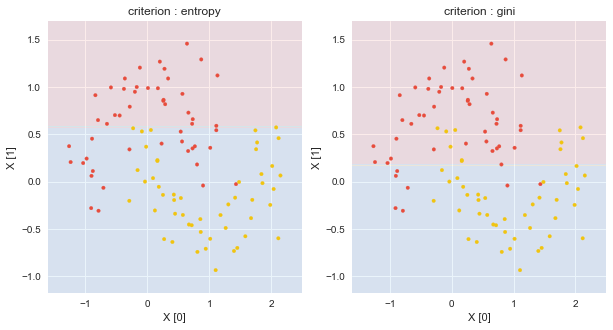
comparison_entropy_gini

scikit-learnのDecisionTreeClassifierのcriterionにginiを設定した結果が以下である．

decision_tree_gini_139 dtc_gini_139

.score() .feature_importances_
0.820 [0. 1.]
0.920 [0.39375244 0.60624756]
1.000 [0.47248044 0.52751956]

今回は，最大深さ9の場合にて，過剰適合を確認することができる．訓練データに対して.score()が1.0であるが，図を見てみると，気持ち悪い分割の仕方をしている部分がある．

scikit-learnのDecisionTreeRegressorで回帰する

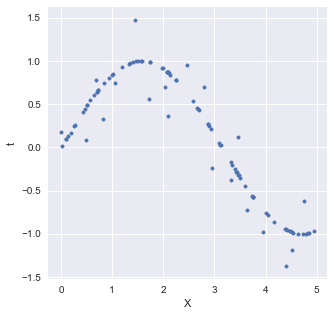
特徴量$X$とラベル $t$ からなる，以下のようなノイズを含んだ正弦波を回帰したい．

sin_wave_with_noise

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap

colors = ['#e74c3c', '#3498db', '#1abc9c', '#9b59b6', '#f1c40f'] # red, blue, green, purple, yellow
cmap = ListedColormap(colors)
plt.style.use('seaborn')

seed = np.random.RandomState(1)
X = np.sort(5 * seed.rand(100, 1), axis=0)
t = np.sin(X).ravel()
t[::5] += 0.5 - seed.rand(20)

plt.figure(figsize=(5,5))
plt.scatter(X, t, marker='.')

plt.xlabel("X")
plt.ylabel("t")
plt.show()

scikit-learnのDecisionTreeRegressorで回帰した結果が以下である．

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap

colors = ['#e74c3c', '#3498db', '#1abc9c', '#9b59b6', '#f1c40f'] # red, blue, green, purple, yellow
cmap = ListedColormap(colors)
plt.style.use('seaborn')

seed = np.random.RandomState(1)
X = np.sort(5 * seed.rand(100, 1), axis=0)
t = np.sin(X).ravel()
t[::5] += 0.5 - seed.rand(20)

from sklearn import tree

fig, ax = plt.subplots(1, 3, figsize = (15, 5))

for max_depth, ax in zip([1,3,9], ax):

    dtr = tree.DecisionTreeRegressor(criterion='mse', max_depth=max_depth)
    dtr.fit(X, t)
    print("accuracy:{:.3f}".format(dtr.score(X, y)))

    N = 1000
    _X = np.zeros((N,1))
    _X[:,0] = np.random.uniform(0, 5.0, N)
    _y = dtr.predict(_X)

    ax.set_title('max_depth : {}'.format(max_depth))
    ax.scatter(X, t, cmap=cmap, marker='.')
    ax.scatter(_X, _y, cmap=cmap, marker='.')
    ax.set_xlabel("X")
    ax.set_ylabel("t")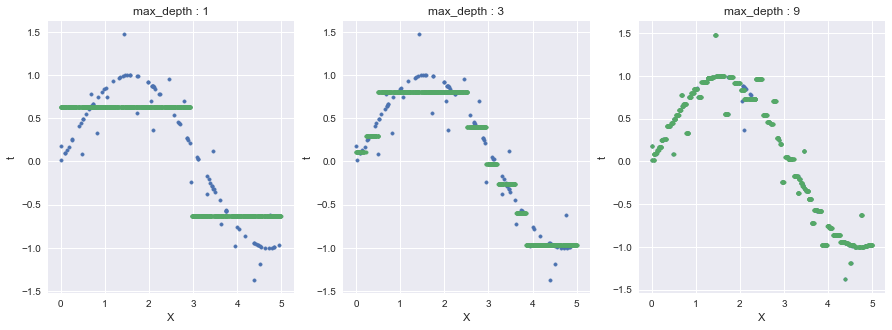

decision_tree_regression_mse_139

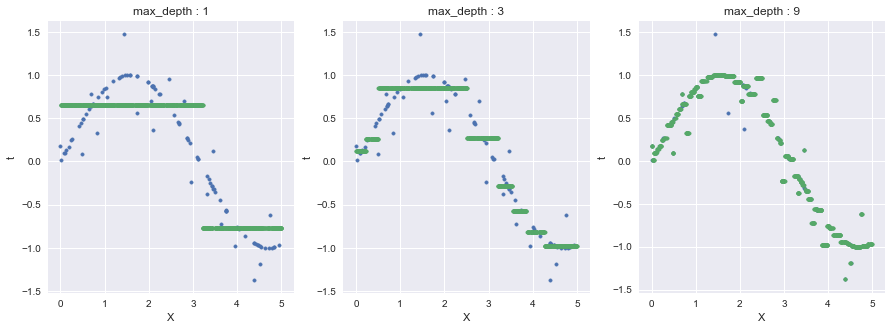
今回はDecisionTreeRegressorのcriterionにmse(Mean Squared Error)を指定している．

緑点がtの予測値であり，最大深さ9の場合においてノイズに過剰適合している部分がある．

平均二乗誤差を基準にして回帰木を構築する

木モデルは，分割軸を特徴空間の軸に沿わせているために，本質的には，準最適となってしまう．特徴軸に対して45度傾いた境界で分割することはできないことに留意する．

上のmax_depth : 1の例では，X=3を閾値として，データ・セットを左右に分割している．

回帰木において，ノードm内の最適な予測値 $y(m)$ は，以下のようなノード内の平均値としている． $x_i$ は特徴量，Rmはノードm内のデータ集合，Nmはノードmに属するすべてのデータ数を表す．

$$ y(m) = \frac{1}{N_m} \sum_{x_i \in R_m} t_i $$

ノードmに関する平均二乗誤差(Mean Squared Error)は以下の式で求められる．ノードm内のデータに関して， $y(m)$ からのばらつきを表現するものである．

$$ H[X_m] = \frac{1}{N_m} \sum_{x_i \in R_m} (t_i - y(m))^2 $$

分割によってできた２つのノードに対し， $H[X_m]$ をそれぞれ計算し，分岐したデータ数で重み付けした和が元ノードのそれよりも小さくなるような閾値をひたすら探していくことで木を構築する．

平均絶対誤差を基準にして回帰木を構築する

ノードmに関する平均絶対誤差(Mean Absolute Error)は以下の式で求められる． $y(m)$ は前述した通りである．

$$ H[X_m] = \frac{1}{N_m} \sum_{x_i \in R_m} |t_i - y(m)| $$

DecisionTreeRegressorのcriterionにmaeを指定した結果が以下である．

decision_tree_regression_mae_139

先程のMSEの場合はノイズに過敏であったが，MAEを用いた場合はノイズに対してロバストになっている．

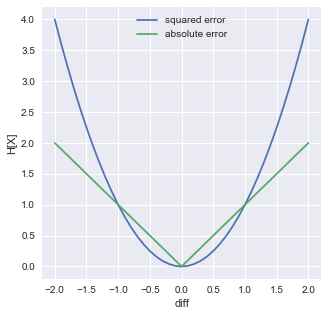
二乗誤差と絶対誤差を比較すると，以下のように誤差(diff)が大きいほど，squared errorは反応しやすいことがわかる．

comparison_squared_absolute

import numpy as np
import matplotlib.pyplot as plt

diff = np.arange(-2,2.1,0.1)
squared = diff**2
absolute = abs(diff)

plt.figure(figsize=(5,5))
plt.plot(diff, squared, label='squared error')
plt.plot(diff, absolute, label='absolute error')
plt.ylabel('H[X]')
plt.xlabel('diff')
plt.legend()
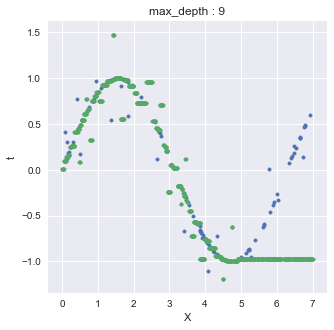
plt.show()

回帰木では外挿(extrapolate)ができないことに注意する

今回の例では，0.0 < X < 5.0 な教師データを用いてDecisionTreeRegressorに学習させたが，このXを超えるようなデータを予測させると以下のようになる．

cant_extrapolate

Appendix. 決定木（ノード）を可視化するために必要なもの

pip install pydotplus
pip install graphviz
brew install graphviz